

If we find two solutions, then any linear combination of these solutions is also a solution. Describing the general form of non homogeneous differential equation and solving it using the superposition method. the independent variables are those of space x, y, z, and time t. An important difference between first-order and second-order equations is that, with second-order equations, we typically need to find two different solutions to the equation to find the general solution. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the general solution to the homogeneous equation and one particular solution. (This is sometimes called the superposition principle.) Another consequence. Just as with first-order differential equations, a general solution (or family of solutions) gives the entire set of solutions to a differential equation. In other words, we want to find a general solution. $$L(f_1+f_2) = L(f_1) + L(f_2) = g_1 + g_2.Īlthough simply finding any solution to a differential equation is important, mathematicians and engineers often want to go beyond finding one solution to a differential equation to finding all solutions to a differential equation. Then $f_1+f_2$ satisfies the equation with source $g_1 + g_2$, since We will see that solving the complementary equation is an important step in solving a nonhomogeneous differential equation.
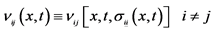
Time-varying magnetic field stimulation of the median and ulnar nerves in the. superposition principle (12), the solution could be written as an in nite linear combination of all the solutions of the form (5): u(x t) X1 n1 a ne n2t n(x): Then u(x t) solves the original problem (10) if the coe cients a n satisfy u 0(x) X1 n1 a n n(x): (6) This idea is a generalization of what you know from linear algebra. Suppose $f_1$ satisfies the equation with source $g_1$ (so $L(f_1) = g_1$) and $f_2$ satisfies the equation with source $g_2$. General Solution to a Nonhomogeneous Linear Equation. Polynomial Solutions of Nth Order Non-Homogeneous Differential Equations. Now the principle of superposition does not hold. method is linear superposition principle, it can only solve the linear solution. Either an inhomogeneous ODE or a homogeneous ODE with inhomogeneous BCs.


Chasnov via source content that was edited to the style and standards of.
#Time invariant ode superposition principle nonhomogeneous license#
This page titled 4.2: The Principle of Superposition is shared under a CC BY 3.0 license and was authored, remixed, and/or curated by Jeffrey R. The crucial property is that $L$ be linear, which means that for any two functions $f_1$, $f_2$ and any real number $c$ we have problem of various types of linear partial differential equations. We have therefore shown that any linear combination of solutions to the homogeneous linear second-order ode is also a solution. For example, the Gauss equation in electrostatics is of this form, with $f$ the electric field $\mathbf$, $L$ the divergence, and $g = \rho/\epsilon_0$. Where $L$ is some operator and $g$ a given function, which may be zero we typically interpret it as some kind of "source" for $f$. In all cases superposition comes about when the physical quantity is represented by a function $f$ that satisfies an equation of the form Section 4.5: The Superposition Principle and Undetermined Coe cients Revisited The Superposition Principle & General Solutions to Nonhomogeneous DE’s We begin this section with a theorem that will allow us to write general solutions for nonhomogeneous equations. Over time, the heat will di use and approach a ‘steady state’ (equilibrium): u(x) lim t1 u(x t): The key point is that the steady state is a solution to the PDE + BCs that does not depend on time. There are many different versions of the principle of superposition, depending on the area of physics the two most common are superposition in electromagnetism and in quantum mechanics. ow with a time independent source h(x) and temperature xed at both ends at di erent values Aand B.


 0 kommentar(er)
0 kommentar(er)
